기술 문서자료
[CAE] 모션 시뮬레이션에서 중복(Redundancies)이란 무엇이며, 어떤 문제를 발생시키는가?
- 25-04-02 00:00
- 웹스시스템코리아
[CAE] 모션 시뮬레이션에서 중복(Redundancies)이란 무엇이며, 어떤 문제를 발생시키는가?
선행 조건: Mate를 Joint로 변환하고, Joint를 구속 조건으로 변환
Motion 시뮬레이션에서는 해석기가 시뮬레이션에 사용하는 Joint를 직접 정의하지 않습니다.
대신, SOLIDWORKS에서 Mate를 정의하면, 소프트웨어가 이를 Joint 및 Joint Primitive로 변환하여 해석기에 적용합니다.
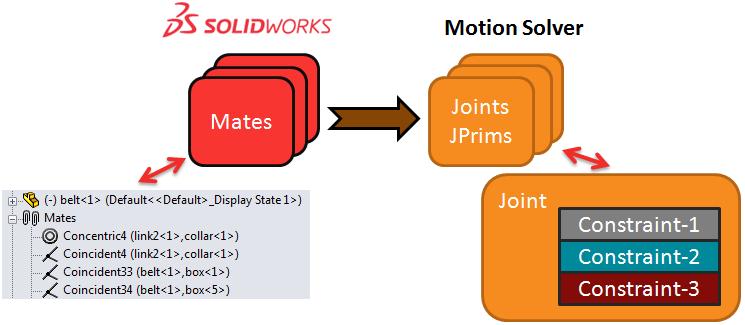
각 Joint 또는 Joint Primitive는 1개에서 6개의 모션 구속을 추가합니다.
예를 들어:
SOLIDWORKS Mate Type |
Geometry 1 |
Geometry 2 |
Motion Joint Type |
No. of Constraints |
Concentric |
Cylinder |
Cylinder |
Cylindrical |
4 |
Coincident |
Point |
Point |
Spherical |
3 |
Line |
Line |
Cylindrical |
4 |
|
Plane |
Plane |
Planar |
3 |
|
Parallel |
Line |
Line |
Parallel Primitive |
2 |
Plane |
Plane |
Parallel Primitive |
2 |
|
Hinge |
Cylinder and Plane |
Cylinder and Plane |
Revolute |
5 |
여유 구속(Redundancies)의 정의
부품을 구속하는 Joint가 정정(Statically Determinate) 상태라면, 반력 분포를 계산하는 것이 가능합니다. 그러나 여유 구속(또는 중복 구속, Redundant Constraints)은 하나의 자유도에 대해 둘 이상의 Joint가 동시에 구속을 가할 때 발생합니다. 이 경우, 기구는 부정정(Indeterminate) 상태가 됩니다.
그 이유는 Motion 시뮬레이션에서 모든 물체가 무한히 강성(Infinite Stiffness) 을 가진다고 가정되기 때문입니다.
예를 들어, 정정 구조물(Statically Determinate Structure) 의 대표적인 예는 세 개의 다리를 가진 테이블입니다. 이 경우, 각 다리가 지면과 접촉하는 지점에서의 힘을 정확히 계산할 수 있습니다. 수학적으로 보면, 미지수(구해야 할 값)와 평형 방정식의 개수가 동일하여 해를 구할 수 있습니다.
반면, 부정정 구조물(Statically Indeterminate Structure) 의 예는 네 개 이상의 다리를 가진 테이블입니다. 대칭성을 고려하여 힘을 추정할 수는 있지만, 수학적으로 보면 미지수의 개수가 평형 방정식보다 많아 단순 계산으로는 정확한 해를 구할 수 없습니다. 이 경우, 유한 요소 해석(Finite Element Analysis, FEA) 을 통해 구조의 강성을 고려한 지지점의 하중 분포를 정확히 구할 수 있습니다.
여유 구속(Redundancies)으로 인한 문제
1. 반력 계산의 문제
기구에 여유 구속(Redundant Constraint) 이 포함되어 있으면, 두 개 이상의 Joint가 하나의 자유도를 제어하려고 충돌하게 됩니다. 단순한 경우에는 해석기가 자동으로 특정 구속 방정식을 제거하여 중복을 해소합니다. 하지만 이 과정에서 하중의 전달 경로가 실제와 다르게 나타날 수 있으며, 그 결과 시뮬레이션에서 계산된 반력 값이 실제와 다르게 나올 수 있습니다.
2. 시뮬레이션 실패 가능성
해석기가 계산을 진행하는 동안, 지속적으로 여유 구속을 재평가하고 이를 제거하여 기구의 운동을 해결합니다. 그러나 특정 시점에서 제거되는 여유 구속이 달라질 수 있으며, 이는 모델의 일관성을 해칠 가능성이 있습니다.
그 이유는 해석기가 기구의 설계 의도(Design Intent)를 이해하지 못하기 때문입니다. 따라서 수학적으로는 타당하지만 기능적으로는 부적절한 구속을 제거할 수도 있습니다. 이로 인해 시뮬레이션이 중간에 실패하거나 예상치 못한 결과가 발생할 수 있습니다.
Joint 여유 구속(Redundancy)이 문제가 되지 않는 경우
1. 운동학적 결과만 관심이 있는 경우
Joint 여유 구속은 다음과 같은 운동학적 결과(kinematic results) 만 분석할 때는 문제가 되지 않습니다.
● 변위(Displacements)
● 속도(Velocities)
● 가속도(Accelerations)
2. 특정 Joint의 힘/토크가 다른 Joint의 힘/토크에 의존하지 않는 경우
예를 들어, Joint 마찰(Joint Friction) 과 같이 특정 Joint의 힘이나 토크가 다른 Joint의 반력에 의존하는 경우가 아니라면, 여유 구속이 있어도 문제가 되지 않습니다.
강성이 반력에 미치는 영향
현실 세계에서 힘의 전달은 하중 경로에 따라 달라집니다. 가장 높은 강성을 가진 경로가 항상 대부분의 하중을 지지하게 됩니다. 그 이유는, 구조가 더 유연할수록 쉽게 변형되므로, 초기에는 자신의 변형을 유발하는 만큼의 하중만을 지지하고, 이후 더 강성이 높은 하중 경로가 확보되면서 주 하중을 지지하게 되기 때문입니다.
사례 1
이를 설명하기 위해, 두 개의 스프링이 위아래로 배치된 경우를 생각해 보겠습니다. 아래쪽 스프링은 위쪽 스프링보다 10배 더 높은 강성을 가지고 있으며, 아래쪽 스프링은 지면에 고정되어 있습니다. 위쪽 스프링에 힘을 가하면, 더 약한 위쪽 스프링이 먼저 변형됩니다. 위쪽 스프링이 최대 압축 한계에 도달하면, 그제서야 더 강성이 높은 아래쪽 스프링이 변형되기 시작합니다.
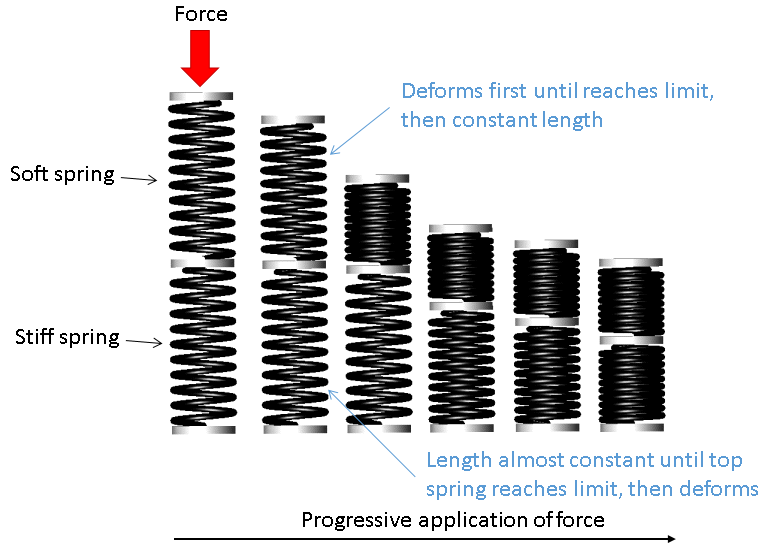
사례 2
이제 가운데 판이 힘을 받고, 위쪽과 아래쪽 판이 움직이지 않는 상황을 가정해 보겠습니다. 아래 그림은 하중이 점진적으로 100N까지 증가할 때 각 스프링에 작용하는 힘을 나타냅니다. 이때, 위쪽 스프링의 강성은 1 N/mm이고, 아래쪽 스프링의 강성은 10 N/mm입니다.
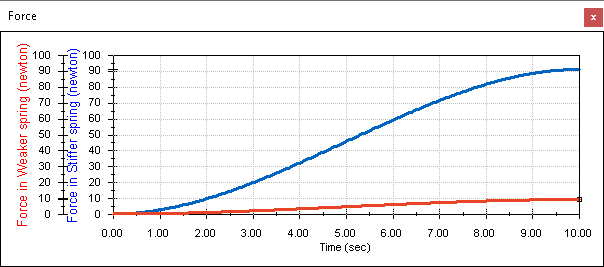
첨부된 예제 모델을 확인해 보십시오.
여유 구속(Redundancies)이 힘 계산에 미치는 영향
여유 구속이 힘에 미치는 영향을 가장 잘 설명할 수 있는 예는 문과 문틀을 연결하는 두 개의 경첩(hinge)입니다.
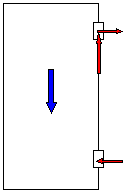
경첩이 하나만 있을 경우, 해당 경첩이 문 전체의 무게를 지지합니다. 하지만 두 개의 경첩이 있을 경우, 두 경첩 사이에서 문 무게가 어떻게 분배될지를 계산하려면 몇 가지 가정이 필요합니다. 대부분의 경우, 문 무게가 두 경첩에 균등하게 분배된다고 가정하지만, 이는 어디까지나 가정일 뿐 실제 상황과 반드시 일치하는 것은 아닙니다.
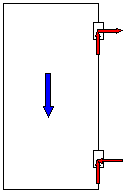
만약 문과 문틀의 두 경첩이 완벽하게 동일한 축 방향 정렬(axial spacing)을 유지하고 있다면, 문에 걸리는 하중이 두 경첩 사이에서 고르게 분배될 가능성이 있습니다. 이것은 문이 유한한 강성을 가지고 있기 때문입니다. 즉, 상단 경첩의 하중 경로가 하중을 받으면서 약간 변형될 경우, 하중의 일부가 하단 경첩을 통해 전달될 수 있습니다.
|
|
문이 상단 힌지에만 의지해 걸려 있음 |
문은 두 개의 힌지에 걸려 있음 |
이제 경첩 위치가 정렬되지 않은 경우를 생각해 보겠습니다. 경첩을 연결하려면 두 부위를 강제로 맞춰야 하며, 이 과정에서 문 경첩이 약간 변형됩니다. 이러한 변형으로 인해 두 경첩 사이에 사전 하중(pre-load) 이 발생합니다. 이 하중은 서로 반대 방향으로 작용하여 전체적인 균형 상태에는 영향을 미치지 않지만, 결과적으로 각 접합부에 작용하는 하중을 증가시키게 됩니다.
만약 세 개의 경첩이 있는 경우, 문제는 더욱 복잡해집니다. 손으로 경첩에 걸리는 하중을 직접 계산하는 것이 어려울 뿐만 아니라, 세 개의 경첩이 완벽하게 정렬되도록 배치하는 것 자체도 어려워 사전 하중이 없는 상태를 유지하기가 쉽지 않습니다.
SOLIDWORKS Motion에서는 모든 부품이 무한히 강성(rigid)한 것으로 간주됩니다. 따라서, 경첩의 위치가 미세하게 어긋나더라도 이를 보정할 유연성이 전혀 없습니다. 그 결과, 두 개의 경첩이 있는 문을 시뮬레이션할 경우, 실제와 달리 하나의 경첩만 문 무게를 지지하게 되고, 나머지 경첩은 수직 하중을 전혀 받지 않게 됩니다. 이것은 솔버가 두 번째 경첩에서 중복된 구속 조건(수직 변위)을 제거하기 때문입니다.
솔버는 어떻게 여유 구속(Redundancies)을 제거하는가?
시뮬레이션을 시작하면, 솔버는 먼저 초기 작업을 수행합니다. 이 작업에서는 기구(mechanism)에 중복 구속이 있는지 감지합니다.
만약 여유 구속이 발견되면, 솔버는 이를 제거하려 시도합니다. 모든 여유 구속이 성공적으로 제거된 경우에만 시뮬레이션이 진행됩니다.
또한, 시뮬레이션이 진행되는 동안 각 시간 단계(time step)마다 솔버는 여유 구속을 다시 평가하고 필요에 따라 제거합니다.
중복 구속 제거 순서
솔버는 다음 순서에 따라 구속을 제거합니다:
1. 회전 구속(Rotational Constraint)
2. 병진 구속(Translational Constraint)
3. 운동 입력(Motion Inputs)
위의 모든 시도가 실패할 경우, 솔버는 중복되거나 일관성이 맞지 않는 구속이 존재함을 알리는 메시지를 출력하며, 기구가 잠긴 상태인지 확인할 것을 권장합니다.
예제: 4절 링크 기구(Four Bar Mechanism)
4절 링크 기구를 예로 들어보겠습니다.
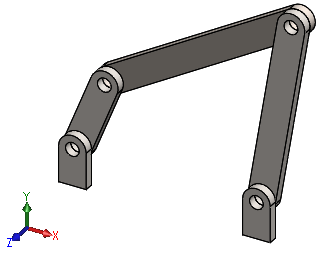
이 기구에서 가운데 있는 세 개의 바(Bar)는 움직이며, 양 끝에 위치한 두 개의 몸체(Body)는 고정되어 있습니다. 각 이동하는 몸체는 총 6개의 자유도(degree of freedom, DOF) 를 가집니다 (병진 3개, 회전 3개). 따라서, 이동하는 모든 부품의 총 자유도는 18개입니다.
이 기구를 조립할 때, 일부 사용자들은 직관적으로 4개의 힌지 구속(Hinge Mate) 을 적용합니다.
각 힌지 구속은 5개의 자유도(병진 3개, 회전 2개)를 제거합니다.
따라서, 4개의 힌지 구속이 총 20개의 자유도를 제거하게 됩니다.
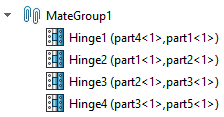
이동하는 바(Bar) 중 하나의 방향(orientation) 만 알면, 기구 내 모든 부품의 위치를 결정할 수 있습니다. 따라서, 최종적으로 이 기구는 하나의 자유도(DOF)를 가집니다.
자유도 계산은 다음과 같습니다:
18 - 1 - 20 = -3
즉, 이 기구에는 3개의 중복 구속(Redundancies) 이 존재합니다. 이 계산에 대한 자세한 설명은 QA00000105478 문서를 참고하세요.
자유도 분석(Degrees of Freedom) 도구는 중복 구속의 개수를 확인하고, 솔버가 중복 구속을 제거하기 위해 억제한(Suppress) 구속 조건을 나열해 줍니다.

첨부된 예제 모델을 참고하세요.
기구에서 중복 구속(Redundancy)을 발생시키지 않도록 Mates(구속 조건)를 정의하는 것이 가능합니다.
예를 들어, 힌지 구속(Hinge Mate) 중 하나를 '점과 축 간의 일치 구속(Coincident Mate)'으로 대체할 수 있습니다.
이러한 구속은 2개의 자유도(병진 2개, 회전 0개)를 제거합니다.
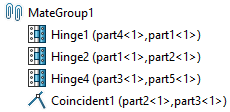
이러한 Mates(구속 조건)를 적용하면, 자유도 분석(Degrees of Freedom) 도구를 통해 중복 구속이 없음을 확인할 수 있습니다.
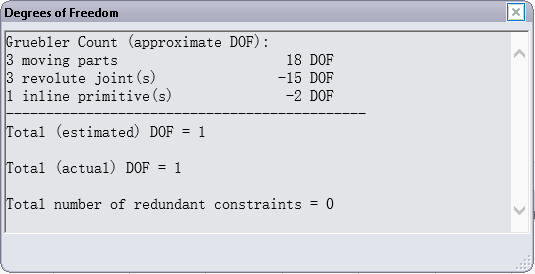
첨부된 예제 모델을 참고하세요.
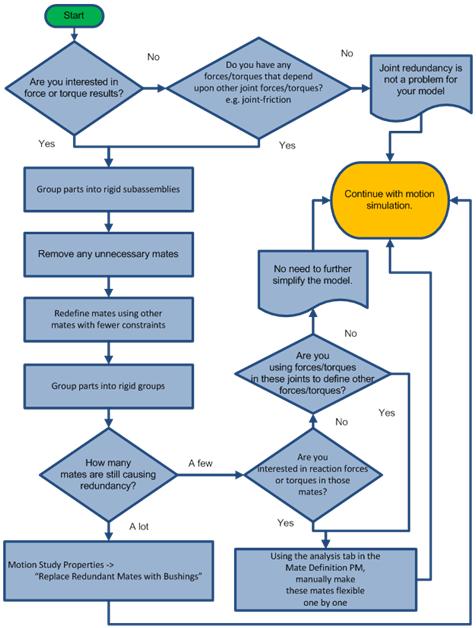
중복 구속(Redundancies) 해결 방법
아래 차트는 중복 구속을 해결하는 절차를 요약한 것입니다..
대표적인 중복 구속 기구(Typical Redundant Mechanisms)
일부 기구들은 구조적으로 중복 구속을 가지는 특성을 지니고 있습니다.
실제 환경에서는 조립 공차(Assembly Tolerance), 유격(Slop), 그리고 강성(Stiffness) 등의 요인으로 인해 이러한 기구가 정상적으로 동작할 수 있습니다.
그러나 수학적으로 해석할 경우, 이러한 기구는 부정확하거나 유효하지 않을 수 있습니다.
다음은 이러한 기구의 대표적인 두 가지 예시입니다.
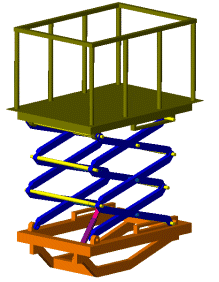
이중 액추에이터(Dual Actuators)로 구동되는 부품
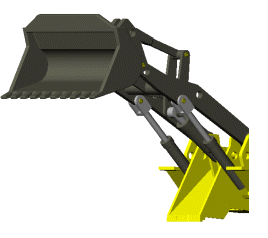
이중 액추에이터(Dual Actuators)로 인한 중복 구속 문제
운동학적(Kinematic) 관점에서 보면, 하나의 액추에이터만 있어도 부품을 움직이는 데 충분합니다.
그러나 실제 설계에서는 좌우 하중을 균형 있게 분배하기 위해 두 개의 액추에이터를 사용하는 경우가 많습니다.
모션 시뮬레이션(Motion Simulation)에서의 주요 문제는 모션(Motion)이 특정 자유도(Degree of Freedom, DOF)에 강제로 변위를 부여한다는 점입니다.
즉, 두 개의 모션을 적용하면 중복 구속이 발생하게 됩니다.
이로 인해 다음과 같은 두 가지 상황이 나타날 수 있습니다.
1. 한쪽 액추에이터만 하중을 지지하고, 다른 액추에이터는 아무 하중도 받지 않는 경우
2. 인공적인(Artificial) 하중이 시스템 내에서 발생하여 액추에이터의 구동력(Driving Force) 결과가 왜곡되는 경우